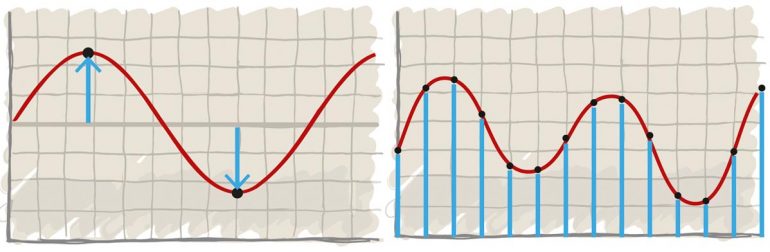
Grundlagen Digital Audio, Teil 1, Samples: Auf null gerundet.
Die Abläufe bei der Wiedergabe digitaler Medien sind für die meisten von uns ein Buch mit sieben Siegeln. Wenn nicht mehr. Lassen Sie uns versuchen, den Nebel zumindest etwas zu lichten. Heute: Samples.
Illustration: Ralf Wolff-Boenisch
Langsam und andächtig strebt der Abtaster seiner Bestimmung entgegen. Sanft taucht die Nadel in eins der Rillentäler, und unverzüglich erleuchtet wohliges Knistern das Zimmer. Es folgt ein Augenblick inspirierender Stille, der das Auditorium in gespannte Erwartung hüllt – für Analogliebhaber und Nostalgiker dürfte dieser Moment ewig währen. „Hach“, (sehnsüchtiger Seufzer), „analog war alles besser“, murmelt derweil ein Zeitgenosse, der via Smartphone-App seine Playlist triggert. Erst passiert nichts, dann folgt eine Pause, und als er gerade beschließt, dass etwas nicht stimmt, fluten die unheimlichen Gizmos in seinen Geräten den Hörraum mit Musik. Die klingt alles andere als schlecht. Eigentlich tönt sie sogar herausragend. Und doch fehlt etwas. Digitalen Audiosignalen geht eben jene Magie ab, die den Umgang mit Vinyl oder einer Bandmaschine zum haptischen Erlebnis macht. Oder noch klarer: Digital Audio hat ein Imageproblem. Und das lässt sich nicht beheben, indem Programme wie Roon abstrakte Daten farbiger und informativer präsentieren oder indem man immer wieder auf die grenzenlosen Möglichkeiten des Webstreamings hinweist. Wir können die Vorgänge hinter einer CD oder einem Stream weder optisch nachvollziehen, noch können wir ihre Komplexität begreifen. Das erzeugt eine Barriere zwischen Mensch und Maschine, die sich nur auf zweierlei Weise beseitigen lässt: durch völlige Ignoranz – Generation Bluetooth ist da auf dem besten Weg – oder durch die Aneignung von Wissen um die (gar nicht so komplizierten) technischen Hintergründe.
Freilich können wir einen derart umfassenden Themenkomplex nicht im Rahmen eines einzelnen Artikels abhandeln. Deshalb fangen wir ganz bescheiden an und befassen uns auf begreifbarem Niveau mit den Basics und den zentralen Problemstellungen der digitalen Signalverarbeitung. Der Rest kommt dann in loser Folge. Und keine Sorge – es soll nicht unser Ziel sein, Ihnen am Ende zu erklären, wie toll Sie Streaming und Co. finden müssen. Richtiger wäre ohnehin der Kehrschluss: Es grenzt an ein technisches Wunder, dass sich Digital Audio überhaupt mit Tonträgern wie der Schallplatte messen kann …
Die Grundlage von allem ist das Binärsystem, unsere einzige Möglichkeit, Zahlen beliebiger Größe mit nur zwei Zuständen abzubilden: Im „an und aus“ der Transistoren eines Prozessors, dem „offen oder geschlossen“ archaischer Lochkarten, dem „reflektierend und blind“ auf der Oberfläche eines optischen Datenträgers oder im ikonischen „null und eins“ abstrahierender Mathematik. Um größere Bandbreiten abzudecken, werden mehrere dieser binären Informationseinheiten kombiniert, wobei die nächsthöhere Binärstelle jeweils dem doppelten Zahlenwert der vorausgegangenen entspricht: 1, 2, 4, 8, 16 … und so weiter. Um eine begreifbare Zahl zu erhalten, muss man die „Werte“ der aktiven Binärstellen einfach summieren. Die Menge der im System verwendeten Informationseinheiten wird als „Wortbreite“ bezeichnet. Bleiben wir der Einfachheit halber bei vier Bit, die immerhin eine Zahlenspanne von 0 (0000) bis 15 (1111) abdecken, insgesamt also 16 Werte darstellen können.
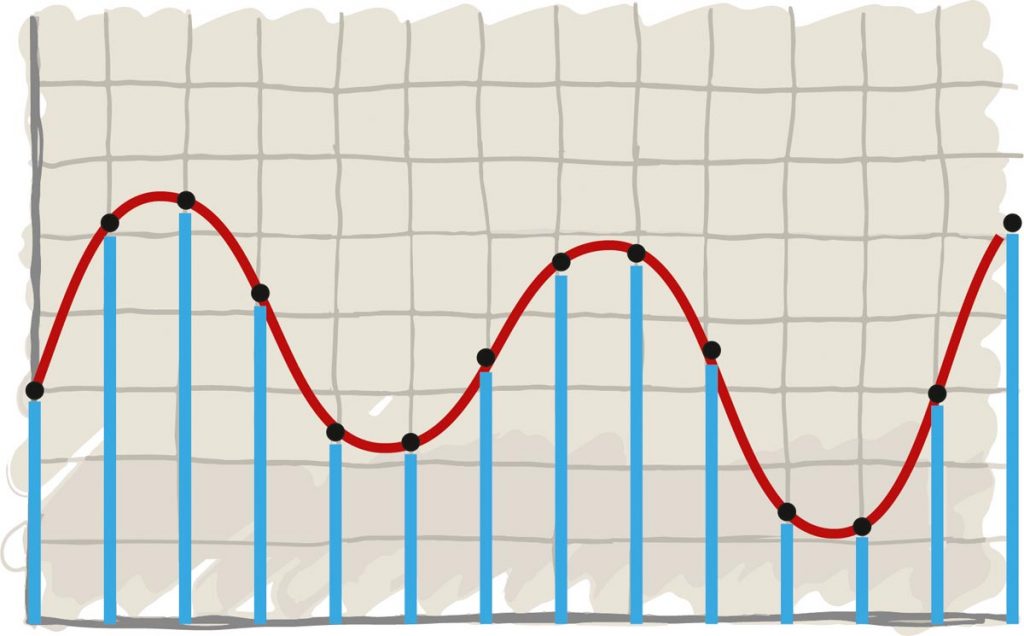
Nun zur Praxis. Machen wir ein Audiosignal binär und anschließend wieder analog: Um elektrische Spannungen in Zahlenwerte zu verwandeln, entnimmt der A/D-Wandler in regelmäßigen Abständen Proben (engl.: „samples“) und übersetzt sie in ihre Binärentsprechungen. Stellen wir uns einfach vor, eine Line-Quelle liefert eine Maximalspannung von 0,8 Volt. Da wir mit einer Wortbreite von vier Bit 16 Werte abbilden können, unterteilen wir die Dynamikbandbreite einfach in Stufen von je 50 Millivolt (800 mV/16). Eine analoge Aussteuerung von 200 mV entspricht damit dem Zahlenwert vier (4 x 50 mV) oder der binären 0010 (nur der Zähler für die Vier ist „an“). 560 mV runden wir entspannt auf 550, was einem Zahlenwert von elf entspricht (11 x 50 mV) oder der binären 1101 (1 + 2 + 8). Schritt für Schritt entsteht eine digitale Audiodatei. Umgekehrt ist das Ganze sogar noch simpler. Stellen wir uns einfach vor, wir basteln einen handverdrillten Schaltkreis, dessen Ausgänge vier unterschiedliche Kondensatoren triggern, die Spannungen von 50, 100, 200 und 400 mV abgeben – die elektrischen Entsprechungen unserer Binärzähler. Jagt man nun eine 1010 durch den Prozessor, geben die Kondensatoren insgesamt 250 mV ab (50 mV + 200 mV). Bei einer 1110 gibt das Wandler-Netzwerk 350 mV aus (50 mV + 100 mV + 200 mV). Das ist freilich extrem vereinfacht, doch wie Sie sehen, ist ein D/A-Wandler letztlich eine erstaunlich analoge Angelegenheit.
Genau hier beginnen dann aber auch die Probleme. Das erste resultiert aus der sogenannten Quantisierung, der Rundung von Spannungswerten. Unser Binär/Volt-Netzwerk kann schließlich nur Signale verarbeiten, die sich geradzahlig durch 50 mV teilen lassen. Die oben erwähnten 560 mV werden nach der A/D- und D/A-Wandlung als 550 Volt ausgegeben. Eine Abfolge von 38 mV, 45 mV und 71 mV erscheint nach dem Quantisieren durchgehend als 50 mV. Die Spannungsunterschiede zwischen den Samples werden grob gerastert, jede Feindynamik geht verloren. Die einfachste Lösung liegt im Anheben der Wortbreite. Mit 8 Bit lassen sich bereits 256 Dynamikstufen abbilden, 16 Bit kommen auf rund 65 000 Spannungswerte. Die heute gebräuchlichen 24 Bit können 16,8 Mio. Abstufungen zu Gehör bringen. Rundungsbedingte Verluste haben da keine akustische Relevanz mehr. Trotzdem gilt: Selbst wenn die Quantisierungsfehler unendlich klein geworden sind, sind sie doch immer noch vorhanden.
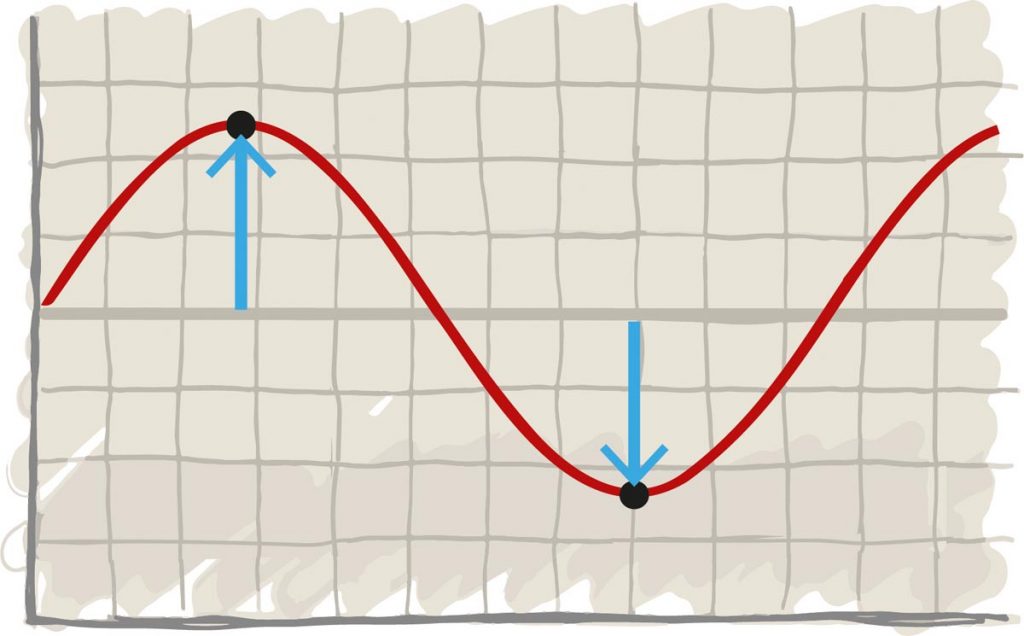
Damit kommen wir zur Taktung beziehungsweise zur zeitlichen Rasterung des Signals. Eine „Clock“ ist meist nichts anderes als ein unter Spannung stabil schwingender Quarzkristall. Dessen Pulsieren im Megahertzbereich wird durch Taktteiler so herunterskaliert, dass man die gewünschte Taktung erhält. 44 100 oder 48 000 Hertz (und ihre Vielfachen) sind gängiger Standard. Die Taktung gibt an, wie oft pro Sekunde die oben geschilderten Prozesse ablaufen. Jedes Mal, wenn das Signal der Clock zu einer neuen Schwingung ansetzt, triggert es damit einen weiteren Abtast- oder Wandlungsdurchlauf. Der binäre Datenstrom einer CD von 44,1 Kilohertz besteht folglich aus 44 100 16-Bit-Samples pro Sekunde. Klingt nach viel, ist es aber eigentlich nicht. Da Schall in der Luft als Druckänderung übertragen wird, folgt auf ein Druckhoch immer ein ausgleichendes Tief. Der Wellendurchlauf einer beliebigen Frequenz besteht daher immer aus zwei Halbwellen – einer positiven und einer negativen. Auch digitale Frequenzen müssen nach der A/D-Wandlung aus mindestens zwei Informationen bestehen. Daraus ergibt sich, dass die höchste abbildbare Tonfrequenz immer der Hälfte des Taktsignals entspricht. Mit 44,1 kHz lassen sich folglich Frequenzen bis 22,05 kHz reproduzieren.
Da das menschliche Gehör bis etwa 20 kHz hinaufreicht, scheint die Rechnung zunächst plausibel. Frequenzen am oberen Ende der Bandbreite müssen bei CD-Audio allerdings mit extrem wenigen Informationen klarkommen, was sie bei der Reproduktion regelrecht entstellt. Das mag bei 20 kHz noch irrelevant sein, jedoch sollte man sich klarmachen, dass eine 10-kHz-Frequenz auch nur aus vier Informationspaketen besteht. Bei den deutlich hörbaren 5 kHz sind es acht, und selbst bei 2,5 kHz geben nur 16 Samples den Ton an. Die Taktung der CD ist also vergleichsweise grob. Vor allem hier liegt der Grund, weshalb die berühmte „HiFi-Triangel“ von CD bisweilen harscher und artifizieller klingt als von analogen Medien. Noch ein weiterer Effekt beeinflusst den Klang digitaler Medien: Elektrische Schaltkreise erzeugen bei der Wiedergabe von Frequenzen komplexe Obertonreihen, die als Geistersignale unter dem Nutzsignal liegen. Man spricht dabei von „Aliasing“. Um diese Frequenzen zu beseitigen, besitzen praktisch alle D/A-Wandler ein Aliasing-Filter im Signalausgang, einen Tiefpass, der nur jene Anteile durchlässt, die wir auch hören wollen. Und wie jedes Filter besitzt auch dieser Tiefpass einen klanglichen Charakter, der enormen Einfluss auf den Tonfall des CD-Spielers, Streamers oder DAT-Recorders hat.
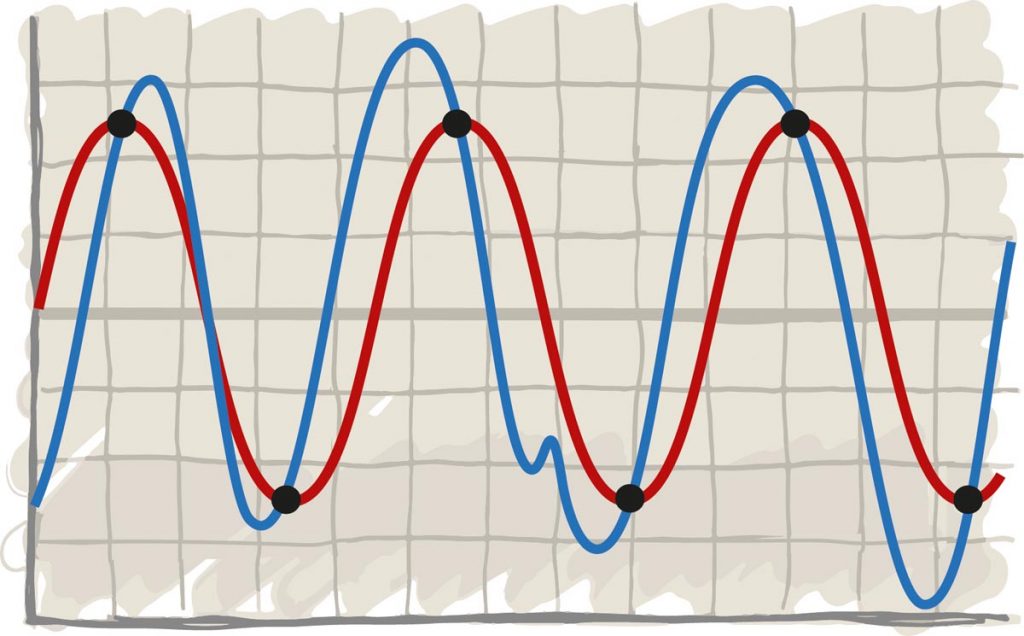
Um sich die Auswirkungen des Aliasing vom Hals zu schaffen, hilft vor allem eins: die Taktrate erhöhen. Ironischerweise wird bei Sample-Frequenzen von 96 oder 192 kHz immer mit der höheren Bandbreite argumentiert. Schließlich können 96 kHz Tonfrequenzen bis 48 kHz und 192 kHz sogar Frequenzen bis 96 kHz einfangen und reproduzieren. Viel wichtiger ist allerdings das, was man nicht hört: das Filter. Dessen Arbeitspunkt kann in Sphären von 50 bis 100 kHz verschoben werden, was seine klangliche Wirkung nicht vollständig beseitigt, aber hörbar mindert. Davon kann sogar die CD profitieren. Via „Oversampling“ wird sie einfach in höhere Taktraten umgerechnet. „4fach-Oversampling“ bedeutet, dass ihre Signale im Wandler mit 176,4 kHz (4 x 44,1 kHz) verarbeitet und entsprechend hochfrequent gefiltert werden. Selbst ein betagtes Digitalmedium kann also noch dazulernen.
Mehr TechTalk? Hier geht’s lang …